Integrated Volatility [IV]

Primary interest centers on forecasting the (latent) integrated volatility over daily and longer inter-daily horizons. Specifically, we define the one-period integrated volatility,

\[IV_{t+1} = \int_{t}^{t+1} \sigma_\tau^2 d\tau\]

and, for \(m\) a positive integer, the corresponding multi-period measure,

\[IV_{t+1:t+m} = \sum_{j=1}^m IV_{t+j}\]

In this context, \(IV_t\) equals the quadratic return variation which, in turn, provides a natural measure of ex-post return variability.

Integrated volatility is not directly observable but, as highlighted by many papers, the corresponding RVs provide consistent estimate of \(IV_t\). The standard RV measure is simply introduced as below.

Realized Volatility [RV]

Realized volatility [RV] is a non-parametric ex-post estimate of the return variation. The most obvious realized volatility measure is the sum of finely-sampledsquared return realizations over a fixed time interval.

\[RV_t^*(h) = \sum_{i=1}^{1/h} r_{t-1+ih}^{*(h)2}\], where \(1/h\) is assumed to be a positive integer and \(r_{t}^{*(h)} = \log(S_t^*)-log(S_{t-s}^*)\). Formally, \(RV_{t}^{*}(h)\) is uniformly consistent for \(IV_t\) as \(h \rightarrow 0\), i.e., the intraday sampling frequency goes to infinity.

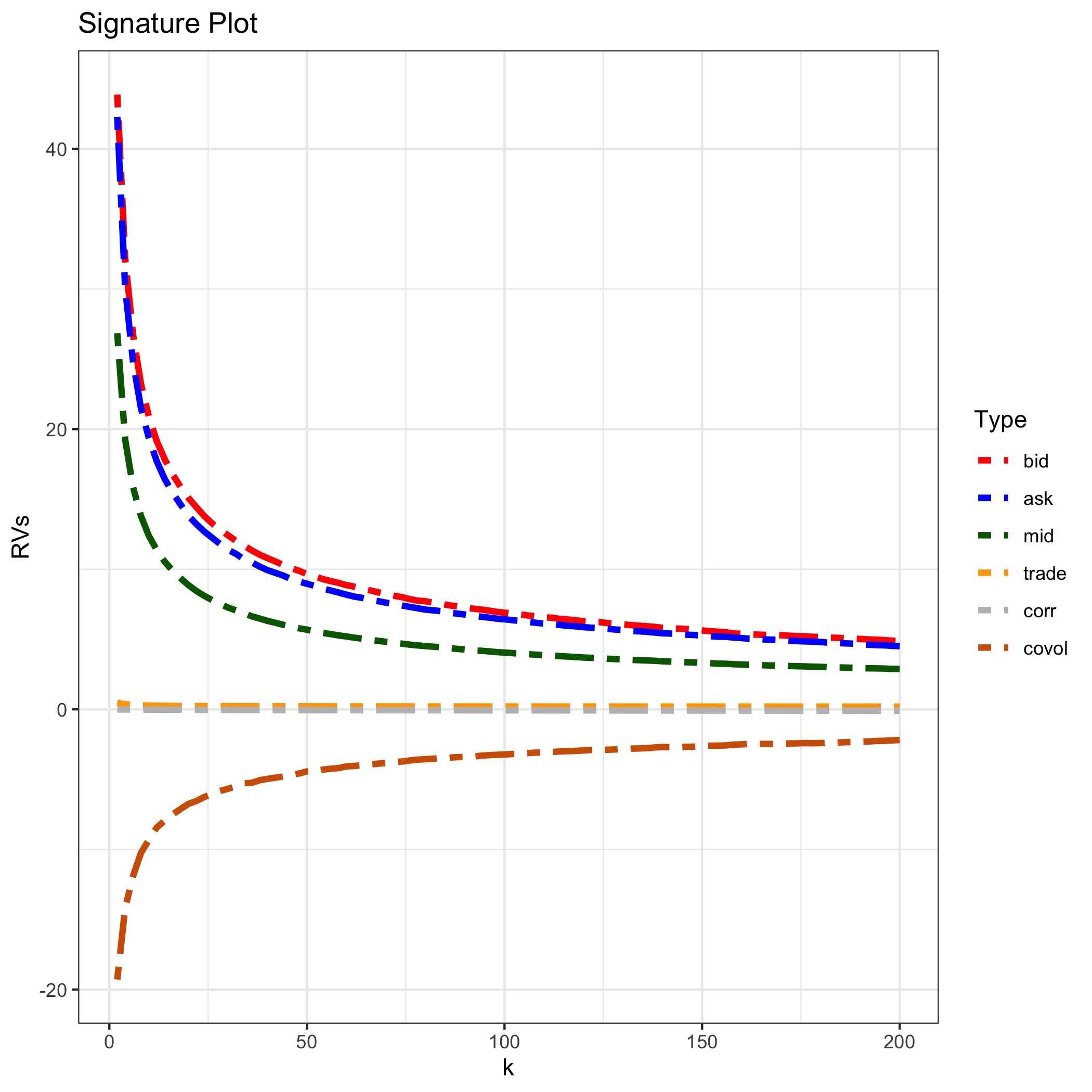
Signature Plot

A microstructure bias, if operative, will probably manifest itself as sampling frequency increases by distorting the average realised volatility. We construct a plot of average realised volatility against sampling frequency, which we call the “volatility signature plot” This helps to reveal the severity of microstructure bias as sampling frequency increases, and can be useful in guiding the selection of sampling frequency. We can also use the volatility signature plots to characterise different market microstructures.

Interestingly, it turns out that the volatility signature has the same form as the variance-time function, which has been extensively studied in finance. However, while there is no information in the volatility signature that is not also present in high-frequency return autocorrelations, the two are complements, not substitutes, as the information relevant for construction and interpretation of realised volatilities is more directly and transparently revealed in the volatility signature plot.

Take log

bid_series = log(quotes2$BID)
ask_series = log(quotes2$ASK)
mid_series = log((quotes2$BID + quotes2$ASK)/2)
price_series = log(trades2$PRICE)

Calculate Averaged Realized Volatility

ARV = function(x, y=x, k){
  #overlap delta(x_i)
  diff_x = diff(x, lag=k)
  diff_y = diff(y, lag=k)
  ARV = sum(diff_x * diff_y) / k
  if (ARV > 0){
    result = sqrt(ARV*250)
  }
  else {
    result = -sqrt(-ARV*250) 
  }
  return(result)
}

Get ARVs for bid,ask,mid, and trade

num_k = 100
step = 2
max_k = num_k * step
ARVs = data.frame(bid = c(1:num_k)*0,
                  ask = c(1:num_k)*0,
                  mid = c(1:num_k)*0,
                  trade = c(1:num_k)*0,
                  covol = c(1:num_k)*0
                  )

for (i in 1:num_k){
  ARVs[i,1] = ARV(bid_series, bid_series, step*i)
  ARVs[i,2] = ARV(ask_series, ask_series, step*i)
  ARVs[i,3] = ARV(mid_series, mid_series, step*i)
  ARVs[i,4] = ARV(price_series, price_series, step*i)
  # Realized Covariation of Bid and Ask
  ARVs[i,5] = ARV(bid_series, ask_series, step*i)
}

ARVs =
  ARVs %>%
  rowwise() %>%
  mutate(corr= covol/(bid*ask))
ARVs['k'] = seq(step,max_k,step)
#ARVs$ID = seq.int(nrow(ARVs))
head(ARVs)

## # A tibble: 6 x 7
## # Rowwise: 
##     bid   ask   mid trade  covol    corr     k
##   <dbl> <dbl> <dbl> <dbl>  <dbl>   <dbl> <dbl>
## 1  40.3  42.2  26.0 0.472 -18.9  -0.0111     2
## 2  28.8  30.0  18.4 0.364 -13.7  -0.0158     4
## 3  23.7  24.7  15.1 0.316 -11.4  -0.0194     6
## 4  20.5  21.5  13.1 0.290  -9.77 -0.0222     8
## 5  18.4  19.3  11.8 0.273  -8.91 -0.0250    10
## 6  16.9  17.7  10.8 0.260  -8.11 -0.0272    12

Plot

Although high-frequency microstructural effects will also be small for sampling intervals larger k, realised volatility estimates constructed from larger return intervals will begin to suffer from a higher sampling error. There is a trade-off between minimising microstructural bias and minimising sampling error

• k가 작을때 = sampling frequency가 매우 큼= highly frequent
• bid/ask RV가 가장 크다
• trasaction price RV 보다 mid quote RV가 더 크다
• sampling frequency가 클때 covariance도 매우 크다

Mystery

• BID와 ASK return series는 같은 방향으로 가야하는거 아닌가?
• MID보다 Transaction Price의 RV가 더 커야하는거 아닌가?

Clue

• Spread Plot

• Bid Plot